M. April Fools' Problem (easy)

time limit per test

2 seconds

memory limit per test

256 megabytes

input

standard input

output

standard output

The marmots have prepared a very easy problem for this year's HC2 – this one. It involves numbers n, k and a sequence of n positive integers a1, a2, ..., an. They also came up with a beautiful and riveting story for the problem statement. It explains what the input means, what the program should output, and it also reads like a good criminal.

However I, Heidi, will have none of that. As my joke for today, I am removing the story from the statement and replacing it with these two unhelpful paragraphs. Now solve the problem, fools!

Input

The first line of the input contains two space-separated integers n and k (1 ≤ k ≤ n ≤ 2200). The second line contains n space-separated integers a1, ..., an (1 ≤ ai ≤ 104).

Output

Output one number.

Examples

input

8 5 1 1 1 1 1 1 1 1

output

5

input

10 3 16 8 2 4 512 256 32 128 64 1

output

7

input

5 1 20 10 50 30 46

output

10

input

6 6 6 6 6 6 6 6

output

36

input

1 1 100

output

100

 

 

Eazy：这个。。一股April Fools Day Contest 的感觉

就是输出最小的k个数的和

怎么发现的呢

因为7这个数只能这么用2的幂次凑出来啊。。

 

N. April Fools' Problem (medium)

time limit per test

4 seconds

memory limit per test

256 megabytes

input

standard input

output

standard output

The marmots need to prepare k problems for HC2 over n days. Each problem, once prepared, also has to be printed.

The preparation of a problem on day i (at most one per day) costs ai CHF, and the printing of a problem on day i (also at most one per day) costs bi CHF. Of course, a problem cannot be printed before it has been prepared (but doing both on the same day is fine).

What is the minimum cost of preparation and printing?

Input

The first line of input contains two space-separated integers n and k (1 ≤ k ≤ n ≤ 2200). The second line contains n space-separated integers a1, ..., an (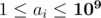) — the preparation costs. The third line contains n space-separated integers b1, ..., bn (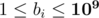) — the printing costs.

Output

Output the minimum cost of preparation and printing k problems — that is, the minimum possible sum ai1 + ai2 + ... + aik + bj1 + bj2 + ... + bjk, where 1 ≤ i1 < i2 < ... < ik ≤ n, 1 ≤ j1 < j2 < ... < jk ≤ n and i1 ≤ j1, i2 ≤ j2, ..., ik ≤ jk.

Example

input

8 4 3 8 7 9 9 4 6 8 2 5 9 4 3 8 9 1

output

32

Note

In the sample testcase, one optimum solution is to prepare the first problem on day 1 and print it on day 1, prepare the second problem on day 2 and print it on day 4, prepare the third problem on day 3 and print it on day 5, and prepare the fourth problem on day 6 and print it on day 8.

Medium：简单的费用流，每天一个点，向后一天连(INF,0)，s向每一天连(1,a[i])，每一天向t连(1,b[i])，增广k次

 

Hard：感受绝望吧！n,k<=500,000

要命了，费用流跑500,000，不会做，看题解

官方的题解是这样的：

我们考虑费用流进行的过程，它相当于是每次选一对i,j使得a[i]+b[j]最小并且合法

怎么叫合法呢？就是此时s->i->j->t这条路径能流通

显然如果i<=j，总是合法，如果i>j，那只有之前i->j这段弧里有正流量才合法

我们可以用一个什么二维数据结构模拟这个过程，比如说线段树

但是非常难写，官方题解里这个线段树要维护13个值

评论区有大神给出了这样的做法：

我们现在先不考虑k，假设a[i]和b[i]可以是负的，我们希望求一个最小匹配

KM本来是n^3的，但是注意到这个图有一个性质，这是半个完全图，观察可以发现，通过交换可以使得最终的最小匹配里不允许有相交的边，于是我们可以有一个dp

设dp[i][j]表示上边匹配到i，下边匹配到j的最小权值

于是我们可以n^2dp求出这个最小匹配

现在我们需要加入k这个限制条件，当然，我们可以给dp加一维，但这样复杂度又退化成n^3了，其实不用这样，我们有一个完美而潇洒的方法来去除k这个限制

如果用刚才的n^2 dp，我们可以很轻松的顺便求出最终匹配里一共有多少对匹配

考虑给每个a[i]和b[i]加上一个d，注意都加上一个数不会影响相对大小，也就不会影响答案正确性

如果d是正无穷，那显然最优匹配是一个都不取

如果d是负无穷，那显然最优匹配是所有的都选

在d不断变大的时候，最优匹配里的匹配对数就不断减少

于是我们可以二分这个d，当选出对数==k的时候就是我们想要的答案，再减去2kd就行了

这样我们就有一个n^2logINF的做法，足以通过medium，但还不足以解决hard，需要进一步优化

继续考虑这个匹配图的性质，我们发现这个好像可以贪心（我不会证明，原创者也不会，cf上也没人帮助证明）

每次加入一个b的时候，我们有三种策略

1、在之前找一个最小的没匹配过的a与这个b匹配

2、用这个b交换一个之前匹配过最大的的b

3、什么都不做

在这三种策略中选最优即可，用一个数据结构维护最小的a和最大的b即可，最终复杂度nlognlogINF

后记：这个二分d比较值得学习，但是这个贪心是怎么想到的？

1 #include 
         
            2 #include 
          
             3 #include 
           
              4 #include 
            
               5 #include 
             
                6 #include 
              
                7 #include 
               
                 8 #include